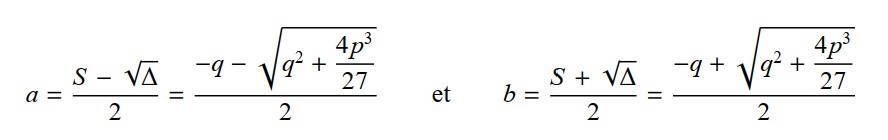
Equations du 3è degré

Jean Pakhomoff

Au cours de mes travaux sur la gnomonique je n’ai pas eu l’occasion d’être confronté à un système demandant la résolution d’une équation du 3è degré.

C’est un problème de géométrie trouvé sur la chaîne youtube de Valéry Kasakov, paraissant assez simple de prime abord, qui m’a permis d’approfondir mes connaissances mathématiques par l’étude de ce type d’équations.

1) Résolution par la méthode des racines évidentes.

Soit k une racine du polynôme ax³+bx²+cx+d. Divisons ce polynôme par a, on a alors

x³+bx²/a+cx/a+d/a=0 pour x=k   posons b/a=u, c/a=v et d/a=w  on écrit alors

x³+ux²+vx+w=0. K étant racine on a x-k=0

Factorisons alors ce polynôme de degré 3 par (x-k). On obtient un second polynôme de degré 2 que nous pouvons écrire x²+px+q.

On a alors (x-k) (x²+px+q) = 0.    En développant cette expression on obtient

x³+px²+qx-kx²-kpx-kq=0 ou encore x³+(p-k)x²+(q-kp)x-kq   donc

x³+ux²+vx+w=0=x³+(p-k)x²+(q-kp)x-kq   en comparant ces deux équations on tire

p-k=u et p=u+k    q-kp=v et q=v+kp    et -kq=w  

On a ainsi les facteurs du polynôme du second degré que l'on peut écrire ainsi:

(u+k)x²+(v+kp)x-kq=o dont nous pouvons connaître les deux racines

Avec delta=sqr((v+kp)²-4(u+k)(-kq))

x'=(-(v+k)-delta)/2 et x''=(-(v+k)+delta)/2

On a ainsi les 3 racines du polynôme: x=k, x' et x''

1^er Exemple:

soit le polynôme x³ −6x² +7x+4. Après quelques essais on trouve la racine évidente x=4=k   ici u=-6, v=7 et w=4  on a alors p=u+k=-6+4=-2

q=v+kp=7+4*-2=-1 et x²+px+qóx²-2x-1

donc x³+ux²+vx+w=(x-4)( x²-2x-1)   3 racines: x=4, x'=1+sqr2, x''=1-sqr2

2è exemple:

soit le polynôme 3x³-12x²-9x+42=0   divisons par 3 on a

x³-4x²-3x+14=0   on peut chercher les racines évidentes parmi les diviseurs de 14: 1,2,7 et 14. 2 fait office de racine évidente. On peut alors écrire:

x³-4x²-3x+14=0=(x-2)'x²+px+q)   on a vu que p=u+k donc p=-4+2=-2

De même q=v+kp alors q=-3+2*-2=-7   on peut alors écrire

x³-4x²-3x+14=0=(x-2)(x²-2x-7)    donc 3 racines: 2, 1+2sqr2, 1-2sqr2

Essai avec x=5

2x³-5x²-10x-75=0    divisons par 2: on obtient x³-2.5x²-5x-37.5=0

Après quelques essais avec les diviseurs de 75 on trouve la racine évidente x=5=k

On aura donc x³-2.5x²-5x-37.5=0=(x-5)(x²+px+q) ou encore

x³-2.5x²-5x-37.5=0=x³+px²+qx-5x²-5px-5q=x³+(p-5)x²+(q-5p)x-5q

p=u+k donc p=-2.5+5=2.5   q=v+kp et q=-5+5*2.5=7.5

On aura donc  (x-5)(x²+2.5x+7.5)=0

Il n'y a que la racine réelle 5 valable, celles du polynôme de second degré étant complexes.

Il n'est cependant pas toujours possible de trouver une racine évidente k de façon à factoriser par x-k. Des mathématiciens du XVIè siècle (Cardan, Tartaglia, Bombelli…) ont imaginé un processus permettant de trouver une racine à une telle équation.

2) Transformation de l'équation origine en équation de forme réduite

Pour cela il est nécessaire de transformer l'équation origine ax³+bx²+cx+d=0 en une équation simplifiée après avoir éliminé les termes en x².

Divisons ce polynôme par a on obtient x³+bx²/a+cx/a+d/a=0

Posons b/a=b', c/a=c' et d/a=d' on obtient x³+b'x²+c'x+d'=0

On fait alors un changement de variable en posant X=x-z alors x=X+z

Et on réécrit l'équation comme (X+z)³+b'(X+z)²+c'( X+z)+d'=0

x3=(X+z)³=(X+z)(X+z)²=X³+2X²z+Xz²+zX²+2Xz²+z³=X³+3X²z+3Xz²+z³

b'(X+z)²=b'X²+2b'Xz+b'z²

L'élimination des termes en X² dans l'addition des polynômes ci-dessus

2X²z+zX²+b'X² =3X²z+b'X² nécessitera d'avoir pour z la valeur -b'/3.

On remplace alors z par sa valeur dans les développements ci-dessous et on réécrit l'équation de cette façon sachant que (u-v)³=(u-v)(u-v)²=(u-v)(u²-2uv+v²)=u³-2u²v+uv²-vu²+2uv²-v³=u3-3u²v+3uv²-v3

Ici u=X et z=-b'/3   et x=X-b'/3

Donc   (X-b'/3)³=X³-3X²(b'/3)+3X(b'/3)²-(b'/3)³=X³-X²b'+(Xb'²/3)-(b'/3)³

b'(X-b'/3)²=b'X²-2Xb'²/3+b'³/9     c'( X-b'/3) =c'X-c'b'/3

Au final on a   X3-X²b'+(Xb'²/3)-(b'/3)³+ b'X²-2Xb'²/3+b'³/9+c'X-c'b'/3 + d' =0  

Les termes en X² s'éliminent  et il reste

X³-Xb'²/3+c'X+2b'³/27-c'b'/3 + d'=0  

X³+X(-b'²/3+c') + 2b'³/27- c'b'/3 + d'=0 et au final on a

X³+X(c'-b'²/3)+2b'³/27 - 9c'b'/27 + d'=0

En posant p=( c'-b'²/3) et q=(2b'³ - 9c'b')/27 + d' on obtient l'équation réduite du 3è

degré X³+pX+q=0 qui peut avoir une solution par la formule de Cardan.

Exemple: réduisons 3x³-5x²-8x+3.

On a b'=-5/3, c'=-8/3 et d'=3/3=1   alors p=-8/3-(-5/3)²/3=-3.59259

Et q=-4.61594. L'équation réduite est donc x³-3.59259x - 4.61594

Pour x³+3x²-24x+28=0 on obtient l'équation réduite X³-27X+54=0

La formule de Cardan appliquée comme nous le verrons ci-dessous donne la racine réelle X=-6.  Mais x=X-b'/3 donc x=-6-3/3=-7

On peut essayer de trouver les 2 autres racines de X dans l'équation réduite en faisant un nouveau changement de variable en posant Y=X+6. Alors X=Y-6 et on réécrit l'équation réduite avec la nouvelle valeur de X. Ce qui donne:

(Y-6)³-27(y-6)+54. Après développement on obtient Y³-18Y²+81Y=0

=Y(Y²-18Y+81) équation dont on trouve facilement les racines: 0 et 9 (racine double)

Donc X=Y-6=-6 et X=9-6=3 Au total l'équation réduite a 2 racines: -6 et 3 (racine double)

ce qui correspond à 2 racines pour l'équation non réduite: x=X+z=X-b'/3=X-1 et

x=-6-1=-7,   x=3-1=2

3) La formule de Cardan.

Un nombre réel peut être considéré comme la somme de 2 autres réels:

7=3+4 ou 5+2…8=4+4 ou 5+3….   De même x=u+v et

x³=(u+v)³=(u+v)(u+v)²=u³+2u²v+uv²+vu²+2uv²+v³=u³+3u²v+3uv²+v³=u³+3uv(u+v)+v^3-

Donc (u+v)³= u³+3uv(u+v)+v³  et (u+v)³-3uv(u+v)-(u³+v³)=0 équation semblable à celle de la forme réduite du polynôme du 3è degré. Ici p=-3uv et q=-(u³+v³)

On pose par commodité de calcul (uv)³=-p³/27 puis u³=a et v³=b

On a donc u³v³=ab et u³+v³=a+b somme S et produit P de 2 nombres.

On apprend au lycée que ces deux nombres sont alors les racines de l'équation du second degré X²-SX+P.  On a donc P=ab et S=-q

Delta=sqr(S²-4P)=sqr((-q)²-4(-p³/27))=sqr(q²+4p³/27)

Si delta >0 il y a deux racines a et b:

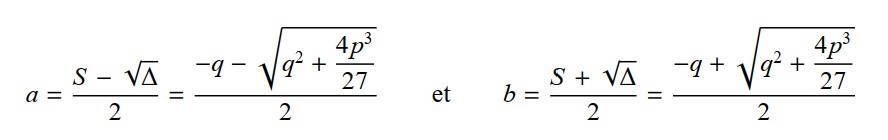
a=u³ et b=v³ donc u=sqr³ a et v=sqr³ b  ce qui revient à écrire puisque X=u+v

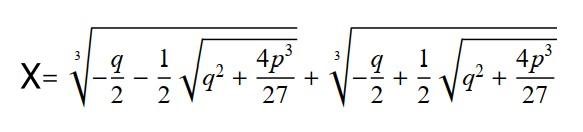
Et en entrant le ½ dans la racine carrée on obtient finalement:

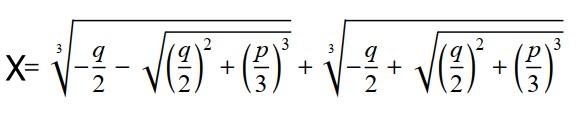
On trouve parfois cette formule écrite de façon quelque peu différente

car établie à partir de x³=-px-q on alors p=-p et q=-q et en remplaçant p et q par leurs nouvelles valeurs on retrouve la précédente formule.

Pour retrouver la valeur x de l'équation non réduite il ne faut pas oublier de rajouter la

valeur b'/3 car on a utilisé la valeur x=X-b'/3 donc x=X+b'/3.

Il est à noter que c'est à partir de ce type d'équation que les mathématiciens du XVIè siècle ont imaginé l'ensemble des nombres complexes.

Pour terminer voici le problème de géométrie trouvé sur la chaîne youtube de Valéry Kasakov.

Problème que je n'aurais pu résoudre sans connaître ce type d'équations.

https://www.youtube.com/watch?v=Cmv3onThkSU

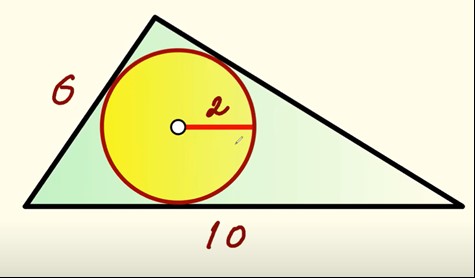
Un triangle dont deux côtés sont égaux à 6 et 10 et le rayon du cercle inscrit est 2.

Quelle est la valeur du 3è côté ?

Ma solution :

x côté à chercher et p demi périmètre du triangle = (6+10+x)/2 et r = 2 rayon du cercle inscrit

La surface du triangle est donnée par S = pr = sqr (p(p-6)(p-10)(p-x)) donc

pr²= (p-6)(p-10)(p-x)) ou encore 4(8+x/2) = 32+2x = (8+x/2 – 2)( 8+x/2 – 10)( 8+x/2 – x)

ce qui donne après développement :   -x³ / 8 + 2 x² - 64 = 0

On procède alors par division de ce polynôme et identification. Puisque l’on a le terme 64 on essaie le diviseur (x-8) et on écrit : (x-8)(ax² +bx+c) = ax³+bx²+cx-8ax²-8bx-8c = ax³ + (b – 8a) x² + (c – 8b) x – 8c = 0

En comparant les équations on peut écrire a = -1/8,  b – 8a = 2  et  b = 2 – 1 = 1,  c – 8b = 0 et c = 8

Au final on a -x³ / 8 + 2 x² - 64 = (x – 8) (-x²/8 + 8) = 0 ce qui nous donne x = 8

https://www.bibmath.net/bios/index.php?action=affiche&quoi=cardan

https://www.youtube.com/watch?v=sZft8S1llTE

https://www.youtube.com/watch?v=GJaB_LLXMsw&t=129s

14 2 2024